Boundary Layer Theory : a Retrospection

2005 was celebrated throughout the world as the year of Physics, because in 1904, the theory of Relativity was postulated by Albert Einstein. By now much have been discussed and done on the theory of relativity, but comparatively less attention has been paid to a sister theory and equally important theory, “The Boundary Layer Theory” born in the same year 1904. Incidentally both the theories had their origin, the same University of Gotingen, Germany, but in two different schools. Albert Einstein was working in the school of Physical Sciences while Ludwig Prandtl, the founder of the Boundary Layer Theory was Director of the School of Aeronatics. Another coincidence about the theories is that the two theories were originally published in German language and later translated into English.

Source : Shutterstock.

The fundamental property of fluid is that it cannot be in equilibrium in a state of stress such that the mutual action between two adjacent parts is oblique to the common Surface. This property is the basis of Hydrostatics and is verified by the complete agreement of the deductions of that science with experiments. Very simple elementary observation is enough, however, to convince us that oblique stresses may exists in fluids in motion. Let us suppose, for instance, that a vessel in the form of a cylinder containing water or other liquid is made to rotate about its axis which is vertical. If the angular velocity of the vessel be constant, the fluid is soon found to be rotating with the vessel as one solid body. If the vessel be now brought to rest, the motion of the liquid continue for some time, but gradually subsides and at length ceases altogether, and it is found that during the process the portions of fluid which are further from the axes lag behind than which are nearer and have thin motion made more rapidly checked. These phenomena point to the existence of mutual action between contiguous elements which are partly tangential to the common surface. For, if the mutual action were everywhere wholly non real, it is obvious that the moment of momentum about the axis of the vessel of any position of fluid bounded by a surface of revolution about this axis would be constant. We infer, moreover, that these tangential stresses are not called into play as long as the fluid moves as a solid body but only whilst a change of shape of some portion of the mass is going on, and that their tendency is to oppose this change of shape. It is usual, however in the first instance to neglect the tangential stress altogether and the fluid is said to be a infect fluid when the tangential stress is absent. To study the special kind of resistance which is met in fluids we employ methods that are of necessity the same as are applicable to the resistance to distortion, known as elasticity which is characteristic of solid bodies. The two classes of phenomena are physically distinct, the latter depending on the actual changes of shape produced, the former on the rate of change of shape but the mathematical methods appropriate to them are to a great extent identical. In analogy to elasticity of solids we attribute ‘viscosity’ of fluids capable of exerting tangential salves.

By stretching a point one could say that the study of viscous fluid flow reaches back into antiquity, for it was probably in prehistoric times that human weaponry developed from simple sticks and stones into streamlined, weighted spears and slim pointed fin-stabilized arrows. One can conclude that primitive recognized and solved in part the problem of viscous resistance. The exact solution for the problem of vicous fluid at rest was covertly given by the Greek mathematician Archimedes (287-212 BC) as his two postulates of buoyancy. Subsequently, in order to derive expressions for the buoyant force on various shaped bodies, Archimedes developed a version of the differential calculus. At about the same time, the Romans were building their magnificent water-supply system and so doing demonstrated same initiative understanding of the effect of viscous resistance in long conduits. In 1500 AC, the equation of curvature of mass for in compressible one dimensional viscous flow was correctly deduced by Leonardo da Vinci, the Italian painter, sculptor, musician, philosopher, anatomist, botanist, geologist, architect, engineer and scientist (perfect man). His notes also contain accurate sketches and description of wave motion, hydraulic jumps, free jets, eddy formation behind bluff bodies, reduction of drag by stress lining and the velocity distribution in a vertex. The first to make a direct study of fluid friction was probably Edone Mariotle (1620 A.C.-1684 A.C.) who invented a balance system to measure the drag of a model held stationary in a moving stream, the first wind tunnel. Mariotle’s Text “Traite movement des caux” was published in 1686, a year before the ‘Principia Mathematica’ of Sir Isaac Newton in 1687. In his ‘Principia’ Newton published the simple statement which delineates the viscous behavior of nearly all common fluids. ‘‘The resistance which arises from the lack of lubricity in the parts of fluid- other things being equal- is proportional to the velocity by which the parts of the fluid are being separated from each other.’’ Such fluids, water and air being prominent examples are now called ‘Newtonian’ in his honor with the Law of linear viscosity thus proposed, Newton contributed the first viscous flow analysis by deriving the correct velocity distribution about a rotating cylinder.

But the world was apparently not ready for viscous flow theory. This was, probably due to Newton himself, because of his more famous discovery, the differential calculus. Whereas these who preceded Newton were essentially limited to discussion of fluid flow problems, those who followed him could use calculus to attack such problems directly. It is natural that the first efforts were directed towards the idealized frictionless fluid. First to succeed was Daniel Bernoulli who in 1738 demonstrated the proportionality between pressure gradient acceleration in inviscid flow. Subsequently Leonherd Euler in 1755 derived the famous Frictionless equation which now bears Bernoulli’s name. Paralleling Euler, Jean d’ Alembert published in 1752 his famous paradox showing that a body immersed in frictionless flow would have zero drag. Shortly afterwards Lagrange (1736-1813 AC), Laplace (1749-1827) and Gerstner (1736-1834) carried the new hydrodynamics to elegant heights of analysis.

But theoretical results such as the d’ Alembert’s paradox were too much for practical Engineers to bear, with the tragic result that fluid mechanics into two parts (1) hydrodynamics under whose banner mathematician soared to new summits and (2) hydraulics which abandoned the theory entirely. This schism continued unhealed for 150 years beginning of the twentieth century. Indeed the separation of fluid mechanic theory from experiment is not extinct even today as witnessed the divergent views of the subject now held between aeronautical, chemical, civil and mechanical engineers. After Euler and his colleagues, the next significant analytical advance was the addition of frictional resistance turns to Euler’s inviscid equations. This was done with varying degree of elegance by Napier (1827), Cand (1825), Poisson (1829), St Venant (1843) and Stocks (1845). The first four treated their equations in terms of an unknown molecular function whereas stocks were the first to use the coefficient of viscosity. Today these equations which are fundamental to the subject are called Napier Stocks equations. The N-S equations through fundamental and rigorous are nonlinear, non-unique, complex and difficult to solve. To this day only a relatively few particular solution have been found of these remarkable equations, Meanwhile the widespread use of digital computers have given birth to many numerical methods and published computations of viscous flows. Experimentation reviews a strong component of viscous flow research, became even the longest super computers are incapable of resolving the fixed details of a high Reynolds number flow.

Towards the end of the 19th century the science of fluid mechanics began to develop in two directions which had practically no points in common. On the one side there was the science of theoretical hydrodynamics which was evolved from Euler`s equation of motion for a frictionless, non viscous fluid and which achieved a high degree of competence. Since, however, the results of this so called chemical science of hydrodynamics stood in glaring contradiction to experimental results it had little practical importance. For this reason practical engineers, prompted by the need to solve the important problem arising from the rapid progress in technology developed their own highly empirical science by hydraulics. This science was based on a large number of experimental data and differed greatly in its methods in its objects from the science of theoretical hydrodynamics. At the beginning of the 20th century Ludwig Pramdtl distinguished himself by showing how to unify these two divergent branches of fluids mechanics. He achieved a high degree of correction between theory and experiment and paved the, way to the remarkably successful development of fluid mechanics which has taken place over the four hundred years. It had been realized even before Prandtl that the discrepancy between the results of classical hydrodynamics and experiments. Moreover, the complete equation of motion for flows with friction (the N-S equation) had been known for a long time. However, owing to the great mathematical difficulties connected with the solution of those equations the way of theoretical treatment of it as fluid motion was barred.

Furthermore, in the case of the two most important fluids, namely, water and air, the viscosity is very small and consequently the forces due to viscous friction are generally speaking, very small compared with the forces like gravity and pressure forces. For this reason it was very difficult to comprehend that the frictional forces omitted from the clinical theory influenced the reaction of a fluid to so large extent.

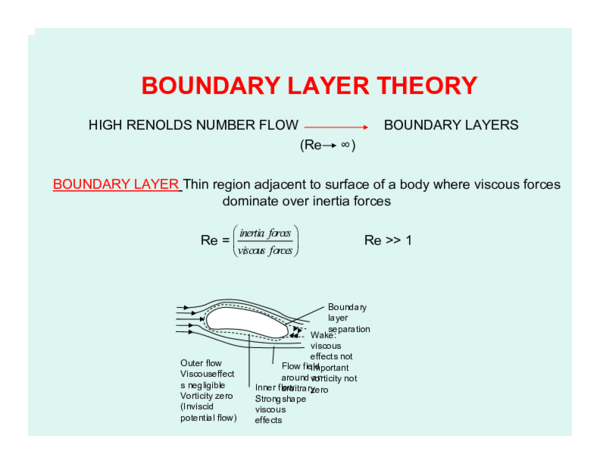
In a paper on ‘‘Fluid motion with very small friction’’ read before the mathematical Congress in Heidelberg in 1904, L. Prandtl showed how to it is possible to analyze viscous flows precisely in cases which had great practical importance. With the aid of theoretical considerations and several simple experiments he proved that the law about a solid body can be divided into two regions, a thin layer in the neighborhood of the body (called body layer) where friction play on essential part and the region outside the layer, where friction may be neglected. On the basis of this hypothesis Prandtl succeeded in giving a physically penetrating explanation on the importance of viscous flows, achieving on the same time a maximum degree of simplification of the mathematical difficulties. The theoretical considerations were even then supported by simple exponents performed in a small water tunnel which Prandtl built with his own hands. He thus took the first step towards a reunification of theory and practice.

Of other works who contributed towards development of the boundary layer theory, mention may be made of Th. Van Kerman, W. Tollmien, H.L. Dryden, A.Betz, H.Schlichling. Subsequently recent works in Great Britain, USA took active part in development of boundary layer theory. Today the study of boundary layer theory has spread all over the world and with other branches it constitutes one of the most important patterns of fluid mechanics.

Author Dr. Gunin C. Sarma served as a teacher in different capacities in Gauhati University, Dibrugarh University, Assam University (Silchar).

[This article was first published in Ganit Bikash (Volume 44, January-June, 2009).]