Introduction to fractional derivatives

Brief introduction:-

In mathematical study, research and development means the extension of previous mathematical methods and definitions. For instance extension of real numbers to complex numbers, extension of factorials to gamma functions etc.

Fractional calculus is the field of mathematics which deals with the study of integrals and derivatives of fractional order. Fractional calculus is nearly as old as conventional calculus. But it is not a popular topic among science and engineering community.

The original question that lead to the fractional calculus was: can the meaning of a derivative of integer order $$frac{d^{n}y}{dx^{n}}$$ be extended to have meaning when n is a fraction?

Leibniz invented the notational $$frac{d^{n}y}{dx^{n}}$$ for nth derivative of $$y=f(x)$$. In 1695, 30 September, L Hospital wrote to Leibniz asking about the value of $$frac{d^{n}y}{dx^{n}}=D^{n}y$$ when $$n=frac{1}{2}$$ ? Leibniz replied, “An apparant paradox from which one day useful consequences will be drawn.” These words are the foundation of fractional calculus.

One of the base function of fractional derivative is the $$Gamma$$ function. $$Gamma(z)$$ is read as gamma of z. Euler’s formula for $$Gamma(z)$$ is given as,

$$Gamma(z)=int_{0}^{infty}e^{-x}x^{z-1}{d}x.$$

If $$Re(z)geq0$$ ; the integral $$Gamma(z)$$ converges absolutely.

Properties of Gamma function:-

From Euler’s formula for $$Gamma(z)$$ we come to know the following relation of gamma function.

Relation 1:-

$$Gamma(z+1)=zGamma(z)$$

Proof:

$$Gamma(z+1)=int_{0}^{infty} e^{-x}x^{(z+1)-1}{d}x$$

$$=int_{0}^{infty}e^{-x}x^{z}{d}x$$

Further solving this integration by parts and putting the limits of the integral we get,

$$Gamma(z+1)=zGamma(z)$$

Relation 2:-

$$Gamma(1)=1$$

Proof:

$$Gamma(1)=int_{0}^{infty}e^{-x}x^{1-1}{d}x$$

$$=int_{0}^{infty}e^{-x}{d}x$$

$$=[frac{e^{-x}}{-1}]_{0}^{infty}$$

$$=1$$

Relation 3:-

$$Gamma (n)=(n-1)!$$

Proof:

From the relation 1 we have,

$$Gamma (n)=(n-1)Gamma (n-1)$$

$$=(n-1)(n-2)Gamma (n-2)$$

$$=(n-1)(n-2)(n-3)dots 3.2.1.Gamma 1$$

$$=(n-1)(n-2)(n-3)dots 3.2.1$$

$$=(n-1)!$$

Relation 4:-

$$Gamma (frac{1}{2})=sqrt{pi}$$

Now, there is a well known relation between $$beta$$ and $$Gamma$$ function,

$$beta (m,n)=frac{Gamma (m)Gamma (n)}{Gamma (m+n)}$$

where, $$beta (m,n)$$ is defined as,

$$beta (m,n)=int_{0}^{1}x^{m-1}(1-x)^{n-1}{d}x$$

Putting $$x=cos^{2}theta$$ in $$beta (m,n),$$

$$beta (m,n)=2int_{0}^{frac{pi}{2}}cos^{2m-1}thetasin^{2n-1}theta{d}theta.$$

Now,

$$beta(frac{1}{2},frac{1}{2})=2int_{0}^{frac{pi}{2}}{d}theta$$

$$=2frac{pi}{2}$$

$$=pi.$$

Therefore,

$$Gamma (frac{1}{2})=sqrt{pi}$$

Notion of fractional derivative:-

In 1819, Lacroix developed a mathematical exercise generalizing from a case of integer order. He took a function $$y=x^{m}$$ , $$min I^{+}$$.

Now,

$$frac{dy}{dx}=mx^{m-1}$$

$$frac{d^{2}y}{dx^{2}}=m(m-1)x^{m-2}$$

Similarly,

$$frac{d^{n}y}{dx^{n}}=m(m-1)(m-2)dots (m-n+1)x^{m-n},$$ $$mgeq n$$

$$frac{d^{n}y}{dx^{n}}=frac{m!}{(m-n)!}x^{m-n},$$ $$mgeq n.$$

And further using gamma function,

$$frac{d^{n}y}{dx^{n}}=frac{Gamma (m+1)}{Gamma (m-n+1)}x^{m-n},$$ $$mgeq n.$$

Now, say $$n=frac{1}{2}$$ and $$m=1$$ then,

$$frac{d^{frac{1}{2}}y}{dx^{frac{1}{2}}}=frac{Gamma 2}{Gamma (1-frac{1}{2}+1)}x^{1-frac{1}{2}}$$

$$=frac{1}{Gamma (frac{3}{2})}x^{frac{1}{2}}$$

$$=frac{2sqrt x}{sqrt{pi}}.$$

Similarly, taking $$n=frac{3}{2}$$ and $$m=3$$ we have,

$$frac{d^{frac{3}{2}}y}{dx^{frac{3}{2}}}=frac{8x^frac{3}{2}}{sqrt{pi}}.$$

Thus we can find the fractional derivative of the function $$y=x^{m},$$ $$min R.$$

We also can find the fractional derivative of the unit function i.e., $$y=1=x^{0}$$ (i.e. m=0).

Therefore,

$$frac{d^{n}y}{dx^{n}}=frac{Gamma 1}{Gamma (n+1)}x^{-n}.$$

It is to be noticed that fractional derivative of a constant function is not equal to zero.

For the identity function $$y=x,$$

$$frac{d^{n}y}{dx^{n}}=frac{x^{1-n}}{Gamma(2-n)}.$$

Fractional derivative of some standard function:-

Exponential function:-

Let us take, $$y=e^{bx}$$

Now,

$$frac{dy}{dx}=b{e^{bx}},$$

$$frac{d^{2}y}{dx^{2}}=b^{2}e^{bx}.$$

Therefore,

$$frac{d^{n}y}{dx^{n}}=b^{n}e^{bx}.$$

For any fractional value of n we have the derivative of the function $$y={e^{bx}}.$$

Sine and cosine function:-

Similarly,

$$frac{d^{n}e^{ibx}}{dx^{n}}=(ib)^{n}e^{ibx}.$$

Simplifying,

$$frac{d^{n}e^{ibx}}{dx^{n}}=b^{n}cos (bx+frac{pi n}{2}) + ib^{n}sin (bx+frac{pi n}{2})$$

$$frac{d^{n}}{dx^{n}}[cos bx + isin bx]=b^{n}cos (bx+frac{pi n}{2}) + ib^{n}sin (bx+frac{pi n}{2})$$

Therefore,

$$frac{d^{n}}{dx^{n}}cos bx=b^{n}cos (bx+frac{pi n}{2})$$

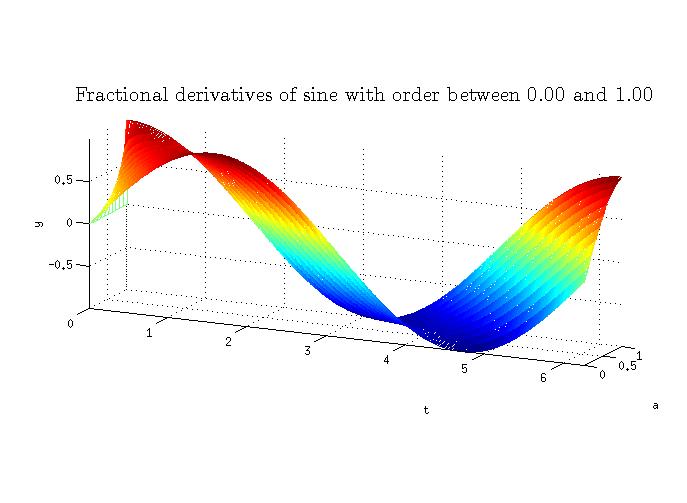
$$frac{d^{n}}{dx^{n}}sin bx=b^{n}sin (bx+frac{pi n}{2})$$

For $$n=frac{1}{2}$$ and $$b=1$$, we have

$$D^{frac{1}{2}}cos x=cos (x+frac{pi}{4})$$

$$D^{frac{1}{2}}sin x=sin (x+frac{pi}{4})$$

Application of fractional calculus:-

Although there is no physical interpretation of fractional calculus for more than 300 years, but now it has been showed that geometric interpretation of fractional integration is “shadows on the wall” and its physical interpretation is “shadows of the past”. There are many application of fractional calculus in the field of physical science, continuum mechanics, signal processing and electromagnetics.

Here some of the applications of fractional calculus are listed.

1) Fractional calculus is applied to the theory of viscoelasticity.

2) It is applied for lateral and longitudinal control of autonomous vehicle.

3) Fractional derivative is used for edge detection.

4) Fractional calculus is used to describe the viscous interaction between fluid and solid structure.

5) It is also applied to find the solution of time-dependent, viscous-diffusion fluid mechanics problems.

Sazid Zamal Hoque,

Tezpur University.