The Genesis of Topology
[In Historical Perspective]
[Creators of Modern Topology]
There are indications that there is growing interest among mathematicians in the history of the development of Mathematics. We believe that the there is reason to be glad with such a tendency. After many hundred years of explosive development, it is worthwhile reflecting on the way mathematics is growing, and therefore the study of the course of the development of the subject with which mathematicians occupy themselves in our days is important. Many of the problems of contemporary mathematics find their roots in classical problems and many old problems are still alive, be it sometimes in a form in which it is difficult to recognize these old problems. It is worthwhile that any mathematician be aware of this fact.
The present article is written from this point of view. Topological ideas are present in many branches of today’s science, particularly in almost all areas of today’s mathematics. The subject of topology itself consists of several different branches, such as point set topology, algebraic topology, differential topology, density topology, analytic topology, manifold topology, knot-topology, chaos-topology, etc. The word “Topology” is derived from two Greek words, “topos” meaning ‘surface’ and “logos” meaning ‘discourse’ or ‘study’. Topology thus literally means ‘the study of surface’ or ‘science of place’. This etymology is, however, inadequate for a clear understanding of the spirit of the subject as it stands today. Topology is sometimes defined as the study of those properties of an object which remain unchanged when that object is subjected to stretching, shrinking, and twisting without tearing, piercing or gluing. Whether a shape is square or round, large or small, is irrelevant in topology, because stretching can change those properties. Topologists ask whether a shape is connected, whether it has holes, whether it is knotted. They imagine surfaces not just in the one-, two-, and three-dimensional universe of Euclid, but in spaces of many dimensions, impossible to visualize. Topology is geometry on robber sheets. It concerns the qualitative rather than the quantitative aspects. It asks, if you do not know the measurements, what can you say about overall structure? Historically, topology developed as an outgrowth of analysis rather than of geometry. However topology resembles geometry very closely in its spirit and indeed can be considered as an abstract form of geometry. We shall trace the rise of topological concepts in a number of different situations:
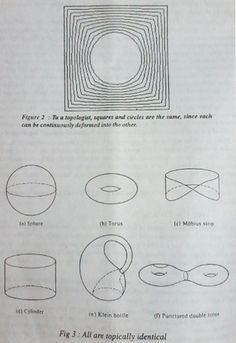
[To a topologist, squares and circles are the same, since each can be continuously deformed into the other. It is said; to a topologist, there is no difference between a tea-cup and a doughnut.]
The movement towards abstraction and generalization in mathematics is a measure of progress towards the notion of a topological space. In this respect, the first work which deserves to be considered as the beginning of topology is due to Leonhard Euler (born on 15 April 1707 in Basel, Switzerland and died on 18 Sept 1783 in Petersburg, Russia). In 1736 Euler published a paper on the solution of Konigsberg bridge problem entitled ‘solutio problematics ad Geometriam Situs Pertinentis’ which translates into English as ‘the solution of a problem relating to the geometry of position’. The title itself indicates that Euler was aware that he was dealing with a different type of geometry where ‘distance’ was not relevant. One can see a diagram of the Konisgsberg Bridge in any graph Theory book. The paper not only shows that the problem of crossing the seven bridges in a single journey is impossible, but generalizes the problem which subsequently gave birth to Graph Theory. The next step in freeing mathematics from being a subject about measurement was also due to Euler. In 1750 he wrote a letter to Christian Goldbach which, as well as commenting on a dispute Goldbach was having with a bookseller, gives Euler’s famous formula for a polyhedron
v-e+f=2
where v is the number of vertices of the polyhedron, e is the number of edges and f is the number of faces. It is interesting to realize that this, really rather simple, formula seems to have been missed by Archimedes and Descartes although both wrote extensively on polyhedral. Again the reason must be that to everyone before Euler, it had been impossible to think of geometrical properties without measurement being involved.
Euler published details of his formula in 1752 in two papers. Euler overlooks some problems with his remarkably clever proof. In particular he assumed that the solids were convex, that is a straight line joining any two points always lies entirely within the solid.
The route started by Euler with his polyhedral formula was followed by a little known mathematician. Antonine-Jean Lhuilier (1750-1840) who worked for most of his life on problems relating to Euler’s formula. In 1813 Lhuilier published an important work. He noticed that Euler’s formula was wrong for solids with holes in term. If a solid has g holes then Lhuiler showed that
v-e+f=2-2g
This was the first known result on a topological invariant.
Mobius published a description of a Mobius band in 1865. He tried to describe ‘one sided’ property of the Mobius band in terms of non-orientability. He through of the surface being covered by oriented triangles. He found that the Mobius band could not be filled with compatibly oriented triangles.
Johann Benedict Listing (1802-1882) was the first to use word ‘topology’. Listing’s topological ideas were due mainly to Gauss, although Gauss himself chose not to publish any work on topology. Listing wrote a paper in 1847 called ‘Vorstudien Zur Toplologie’ although he had already used the word for ten years in correspondence. In 1861 Listing published a very important paper in which he described the Mobius band (4 years before Mobius) and studied components of surfaces and connectivity.
Listing was not the first examine connectivity of surface. Riemann had studied the concept in 1851 and again in 1857 when he introduced the Riemann surface. The problem arose from studying a polynomial equation f(w,z)=0 and considering how the roots vary as w and z vary. Riemann introduced Riemann Surfaces, determined by the function f(w,z) so that the function w(z) defined by the equation f(w,z)=0 is single valued on the surfaces.
Jordan introduced another method for examining the connectivity of a surface. He called a simple closed curve on a surface which does not intersect itself on irreducible circuit if it cannot be continuously transformed into a point. If a general circuit c can be transformed into a system of irreducible circuits $$a_1,a_2,dots ,a_n$$ so that c describes $$a_i$$’s m times then he wrote
$$c=ma_1+ma_2+dots +ma_n.$$
The circuit c is reducible if
$$ma_1+ma_2+dots +ma_n=0$$ ……………… (*)
A system of irreducible circuits $$a_1,a_2,dots ,a_n$$ is called independent if they satisfy no relation of the form (*) and complete if any circuit can be expressed in terms of them. Jordan proved that the number of circuits in a complete independent set is a topological invariant of the surface. Listing had examined connectivity in three dimensional Euclidean space but Betti extended his ideas to n dimensions. This is not straightforward as it might appear since even in three dimensions it is possible to have a surface that cannot be reduced to a point, yet closed curves on the surface can be reduced to a point.
The idea of connectivity was eventually put on a completely rigorous basis by Poincare in a series of papers— Analysis Situs, in 1895. Poincare introduced the concept of homology and gave a more precise definition of the Betti numbers associated with a space than had Betti himself. Euler convex polyhedral formula had been generalized to not necessarily convex polyhedral by Jonquihres in 1890 and now Poincare put it into a completely general setting of a p-dimensional variety V. Also while dealing with connectivity Poincare introduced the fundamental group of variety and the concept of homology was introduced in the same paper of 1895.
A second way in which topology developed was through the generalization of the ideas of convergence. This process really began in 1817 when Bolzano removed the association of convergence with sequence of numbers and associated convergence with any bounded infinite subset of the real numbers.
Cantor in 1872 introduced the concept of the first derived set, of the set of limit points, of a set. He also defined the closed subsets of the real line as subsets containing their first derived set. Cantor also introduced the idea of an open set-another fundamental concept in point set topology. It stems in part from recognition of the fact that many important mathematical topics depend entirely upon the properties of limit points, and sometimes topology may be considered as an abstract study of the limit point concept.
Weierstrass in 1877 in a course of unpublished lectures gave a rigorous proof of the Bolzano Weierstrass theorem which states— “A bounded infinite subsets of S of the real numbers possesses at least one point of accumulation p, i.e. p satisfies the property that given any $$epsilon>0$$ there is an infinite sequence $${p_n}$$ of points of S with $$|p_n-p|<epsilon .$$” Hence the concept of neighbourhood of a point was introduced. Hilbert used the concept of a neighbourhood in 1902 when he answered in the affirmative one of his own questions, namely— ‘Is a continuous transformation group differentiable?’ In 1906 Frechet called a space ‘compact’ if any infinite bounded subset contains a point of accumulation. However Frechet was able to extend the concept of convergence from Euclidean space by defining “metric spaces”. He also Riesz, in a paper to the International Congress of Mathematics in Rome(1909), disposed of the metric completely showed that Cantor’s ideas of open and closed subsets extended naturally to metric space completely and proposed a new axiomatic approach to topology. The definition was based on a set definition of limits points, with no concept of distance. A few years later in 1914, Hausdorff defined neighbourhoods by four axioms, so again there were no metric considerations. This work of Riesz and Hausdorff really allows the definition of abstract topological spaces.
There is a third way in which topological concepts entered mathematics, namely, via functional analysis. This was a topic which arose from mathematical physics and astronomy, brought about because the methods of classical analysis were somewhat inadequate in tackling certain types of problems. Jacob Bernoulli and Johan Bernoulli invented the Calculus of variations where the value of an integral is thought of as a function of the functions being integrated.
Hadamard introduced the word “functional” in 1903 when he studied linear functionals F of the form
$$F(f)=lim_{nrightarrow infty} int _a ^b f(x)g_n(x)dx.$$
Frechet continued the development of functional by defining the derivative of a functional in 1904. Schmidt in 1907 examined the notion of convergence in sequence spaces, extending methods which Hilbert had used in his work on integral equations to generalize the idea of a Fourier series. Distance was defined via an inner product. Schmidt’s work on sequence spaces has analogues in the theory of square summable functions, this work being done also in 1970 by Schmidt himself and independently by Frechet.
A further step in abstraction was taken by Banach in 1932 when he moved from inner product spaces to normed spaces. Banach took Frechet’s linear functionals and showed that they had a natural setting in normal spaces.
An exciting story of evolving the concept of topology in a rigorous way is as follows: In 1887 King Oscar II of Sweden offered a prize of 2,500 crowns for an answer to a functional question in astronomy— “Is the Solar System stable?” Will all the planets continue to move in roughly their current orbits, or could the earth wound off into the cold and dark of Pluto crash into the Sun? Will the Solar System holds the road, or will it slid sideways and crash into the cosmic ditch?” The answer to this question is not so important, but how sensible the question is!
Henri Poincare (French Mathematician, 1854-1912) was a unifier, a seeker of general principles, the last of the traditionalists and the first of the moderns. His study and investigation ranged over virtually all of the mathematics of his age: differential equations, number theory, complex analysis, mechanics, astronomy, mathematical physics. Poincare tried hard to give an acceptable answer to the King Oscar’s problem. He did not solve it; that came much later and the solution was not of the King originally anticipated. But he made such a dent in that he was awarded the prize anyway; and to do it he invented a new brand of mathematics-‘topology’. He called it ‘analysis situs’— the analysis of position. Poincare characterized topology as the mathematics of the general study of continuity. Continuity is the study of smooth, gradual changes, the science of the unbroken. Discontinuities are sudden, dramatic: places where a tiny changes is caused, produces an enormous change in effect— which is the key study of “Dynamical System.” This is why topology and Dynamical System are termed as two sides of one coin. Poincare developed many of his topological methods while studying ordinary differential equations which arose from a study of many astronomy problems. His study of autonomous systems
$$frac{dx}{dt}=f(x,y) frac{dy}{dt}=g(x,y)$$
involved looking at the totality of all solutions rather than at particular trajectories. The collection of methods developed by Poincare was built into a complete topological theory by Brouwer in 1912.
During the twentieth century, there were three revolutions in Physical Sciences, namely the discoveries of “the theory of Relativity”, “the Quantum Theory” and “the Chaos Theory” along with Fractal Geometry”. Around 1950, physical scientists simplified many complicated physical concepts with the aid of topology. Moreover, during that time topology started penetrating into almost all branches of mathematics, and hence the fifties are regarded as the heytime or the golden period of the development of topology. Dimension Theory, knot-Theory and Fractal Geometry are three beautiful daughters of Topology that have provided exciting fields of research in modern times. In conclusion one can say that Topology is a paradigm of the twentieth century trend towards abstraction and axiomatization.
The Fields Medal, the highest honour in Mathematics, has played the role of the Nobel Prize in Mathematics. The Fields Medal was awarded to great Topologists: Kunihiko Kodaira (Princeton University, U.S.A. 1954), Stephen Smale (University of California, U.S.A. 1966) Sege Novikov (Moscow University, Russia, 1970), William P. Thurston (Princeton University, U.S.A. 1982), Michael H. Freedman (University of California, U.S.A. 1986) and Vaughan F.R. Jones (University of California, U.S.A., 1990) for their outstanding work on “Topology”.
Author: Prof. Tarini K. Dutta
Prof. T. K. Dutta is professor of Mathematics in the Department of Mathematics, Guwahati University.
[This article was published in ‘Ganit Bikash’]


