P v/s NP Problem

[Editor’s Note: This is the next part in our series on the Millennium Problems.]

This is a problem in the area of computational complexity which deals with efficiency of algorithms. An alphabet A is a finite nonempty set of symbols and a computational problem over A is simply a function from the set A* of words over A, to A*. In case the range of the function has just two elements typically denoted by 1 and 0 or often by “yes” and “no”, the problem is called a decision problem. Given a computational problem f over A, an element x  A*  is called an input for f and f(x) is called the corresponding output. Solving a problem f means obtaining output f(x) for any given value of the input x. An algorithm for f is a step by step method for solving f in a finite number of steps for any input. Each step has to be a simple step of manipulating a symbol. The allowed steps in an algorithm was clearly defined by Alan Turing by defining a standard machine called the Universal Turing machine and it is believed that any computational task that can be carried out in any computing machine can be carried out on a Turing machine and this machine then gave the first precise definition of an algorithm.

It was then shown that there are decision problems which cannot be solved by algorithms. Using this it was proved that the problem “Given a Diophantine equation i.e. a polynomial equation with integer coefficients, determine whether it has an integer solution.” is not decidable. This settled one of the problems given in Hilbert’s list.

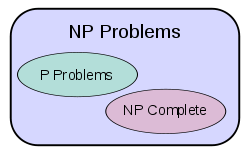
For the scientists working with applications, decidable problems are the only important ones but it was important that the time needed for computation is not prohibitively large. An algorithm is said to be polynomial time if the number of steps required to compute the output for a given input x is bounded by p(|x|) where p is a fixed polynomial and |x| is the size of x i.e. the number of symbols in x. Unless an algorithm is polynomial time, it is useless for practical computation. Accordingly the class P of decidable problems was defined to be the class of decision problems having a polynomial time algorithm. Almost all  the decision problems arising in applications fall in a broader class called the class NP. A decidable problem f is said to be in class NP if there is a fc  P such that f(x) = 1 if and only if there exists cx  A* with fc(x,c) = 1 and |cx|  ≤ q(|x|) for a fixed polynomial q ( an instance is an yes instance if and only if it has a concise certificate which can be checked in polynomial time for validity ). It is easy to prove that P⊆ NP . The question is whether P = NP. The P = NP question was properly formulated by S. Cook in  1971, when he found a class of problems  in NP called the NP-complete problems  which had the property that if f is NP-complete, then given any problem g in NP, g has a polynomial-time reduction to f   i.e.  g = f o r  where  r is polynomial-time. Obviously then P = NP if and only if any NP-complete problem is  in P.

Cook proved that the Satisfiability problem in Propositional Logic is NP-Complete and this was the first problem found to be NP-complete. Since then many other problems have been proved to be NP-complete. One such famous problem is the Hamiltonian Cycle problem. But even after  many repeated attempts by almost all the top Computer Scientists, no one has found a polynomial time algorithm for any NP-complete problem and the current belief is that P ≠  NP. But it is also believed that fresh developments in Mathematics will be required to prove this and therefore this has also been named as a Millennium problem.

[The author is a Professor in the Department of Computer Science and Engineering, Tezpur University, India.]