02 Apr The most beautiful formulae/theorems/identities in mathematics

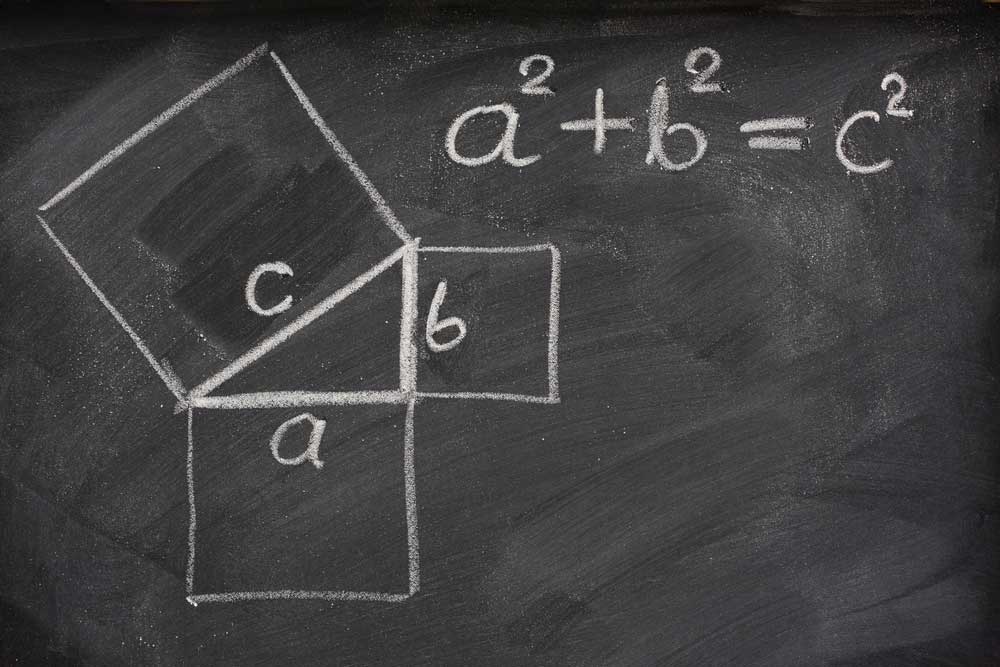
This is my personal collection of formulae/theorems which I consider lovely. By “lovely”, I mean objects which possess a certain degree of Elegance and Simplicity. The formulae/theorems are listed in no particular order.

Pythagoras’ theorem

The most popular and fascinating theorem in Euclidean geometry takes the first place in the list.

If AB, BC and AC are three sides of a right angled triangle  ABC, where AC is the hypotenuse, then

Euler’s formula

, where is the Euler’s number.

Heron’s formula

. where is the area of a triangle whose sides are of length and perimeter is .

Bayes theorem

Or

 

Sine rule
If A,B,C are vertices of a triangle, and sides a,b,c are a = BC, b = CA, c = AB then

Cayley – Hamilton theorem

every square matrix over a commutative ring (such as the real  or complex field) satisfies its own characteristic equation.

Euclid’s algorithm

If a and b are integers and a > b, then gcd(a, b) = gcd(a (mod b), b)

Trigonometric gem 1

sin(x – y) sin(x + y) = (sin(x) – sin(y)) (sin(x) + sin(y))

Trigonometric gem 2

X+Y+Z = XYZ if
X = tan(A)
Y = tan(B)
Z = tan(C)

and

Of course, this list is undeniably incomplete. There will be more entries, as I discover more gems.

Download this post as PDF (will not include images and mathematical symbols).