Real Analysis

Weirstrass' M-Test

Manjil Saikia

Nov 30, 2011 • 2 min read

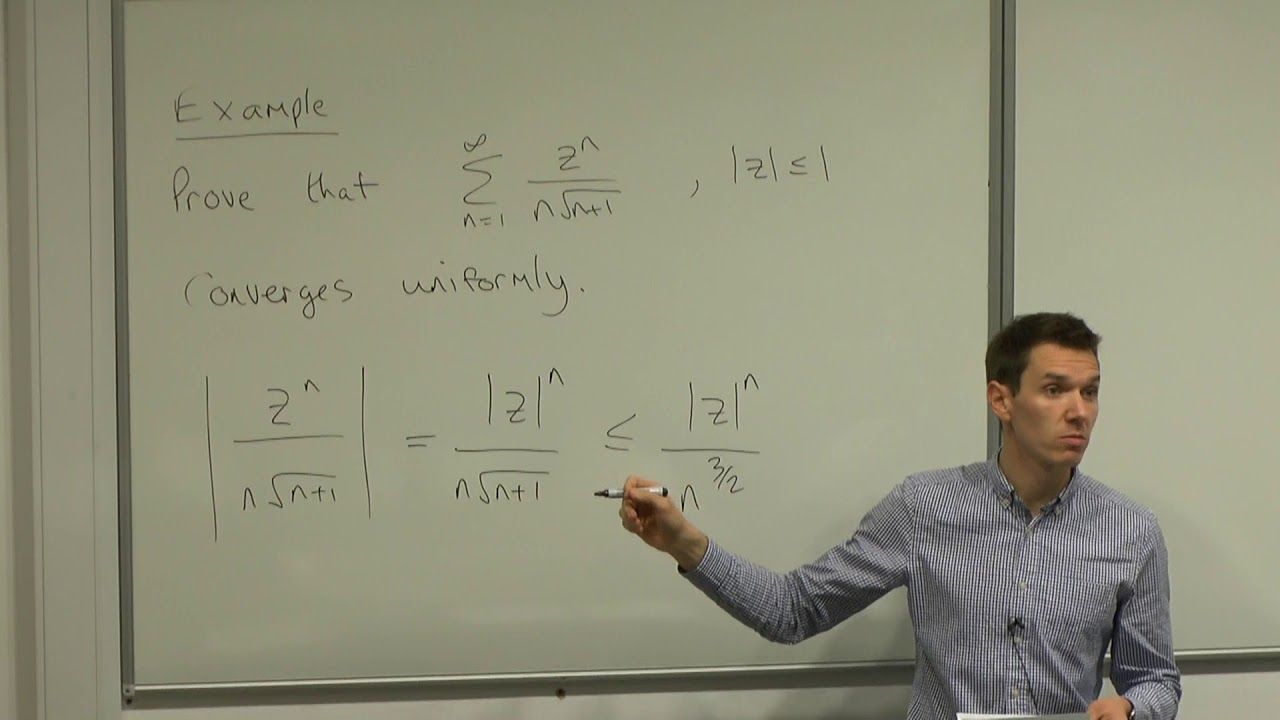
We shall state and prove a very important result in Real Analysis called the Weirstrass’ M-Test. The statement of the theorem is given below.

Let $\{M_n\}_{n\geq 0}$ be a sequence of positive real numbers such that $\mid f_n(x) \mid \leq M_n$ for $x \in D$ , $n \in N$ . If the series $\sum M_n$ is convergent, then $\sum f_n$ is uniformly convergent on $D$ .

We prove the result as follows:

If $m>n$ , we have the relation,

$\mid f_{n+1}(x)+\cdots+f_m(x)\mid \leq M_{n+1}+\cdots+M_m,~for~x\in D$ .

Since $\sum M_n$ is convergent so there exists some $n^{\prime} \in N$ such that,

$\mid M_{n+1}+\cdots+M_m \mid \leq \epsilon, ~ \forall m >n^{\prime}.$

The above relations imply,

$\mid f_{n+1}(x)+\cdots+f_m(x)\mid < \epsilon.$

It is thus clear now that $\sum f_n$ is uniformly convergent on $D$ .

There are other variants of this result, which is left for a later post.

Sign up for more like this.