The Fourier Transform: Bridging Theory and Applications in Signal Processing, Music Synthesis, and Climate Analytics

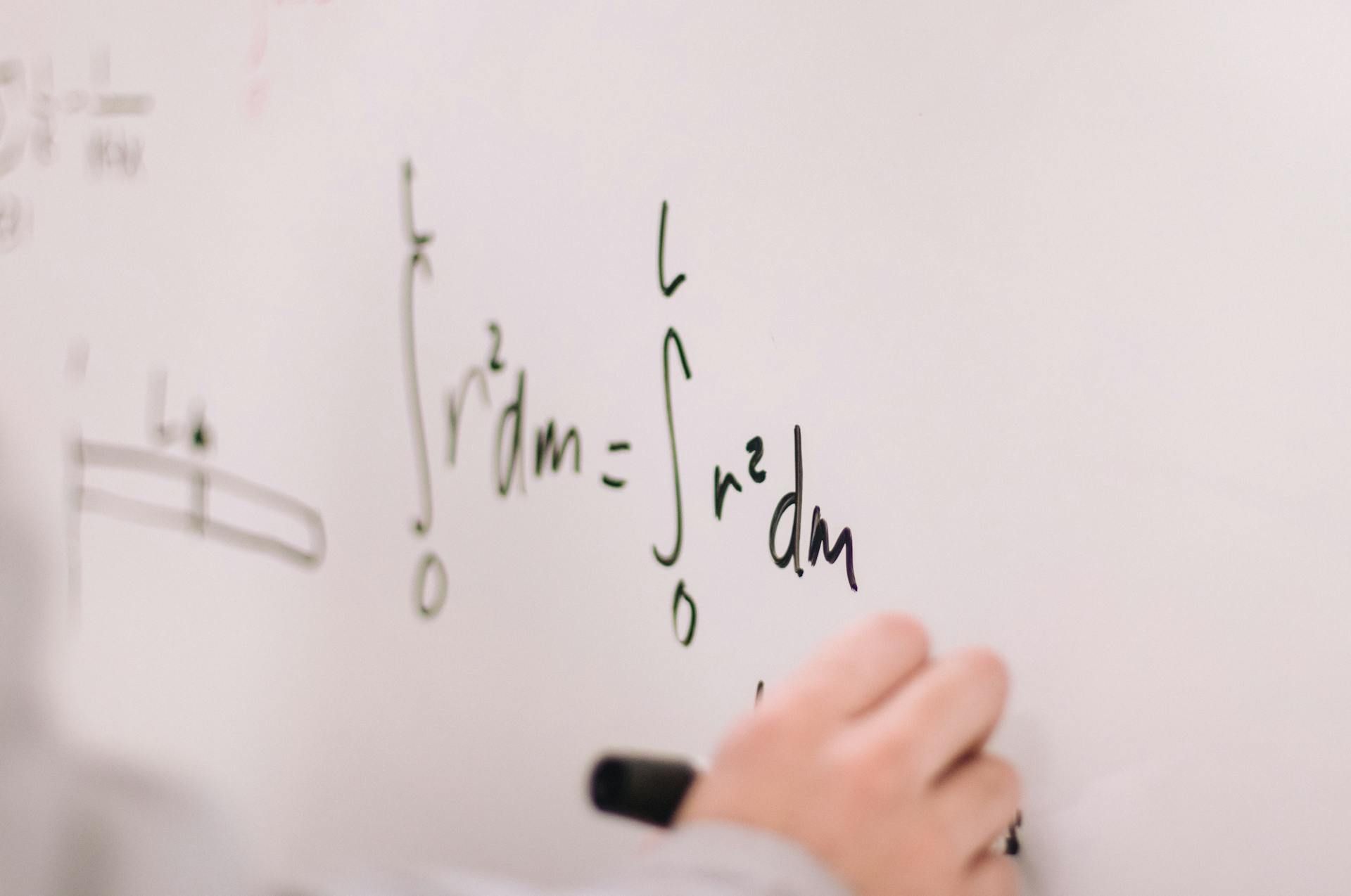
The author Arhaan Goyal is a student of Jayshree Periwal International School, Class of 2025, and can be reached at arhaangoyal[at]gmail.com.

This paper below explores the fundamental concepts and applications of the Fourier Transform, a convolution tool in mathematics, physics, and engineering. By establishing the connection between the Taylor series, Fourier series, and the Fourier Transform, we provide a solid foundation for understanding the transform's versatility. The paper highlights the expansion of the Fourier Transform, which is analogous to the Taylor series expansion, and utilizes orthogonality properties of the Fourier series representation. The paper also explores the applications of the Fourier Transform in signal processing, music synthesizing, and climate analytics.