A theorem on right angled triangles

Theorem: In a Right-Angled Triangle with sides in A.P. Series, the distance between the point of intersection of median & altitude at the base is 1/10^th the sum of other two sides.

This Theorem applies in Two Conditions:

1. The Triangle must be Right-Angled.
2. Its Sides are in A.P. Series.

We Have:

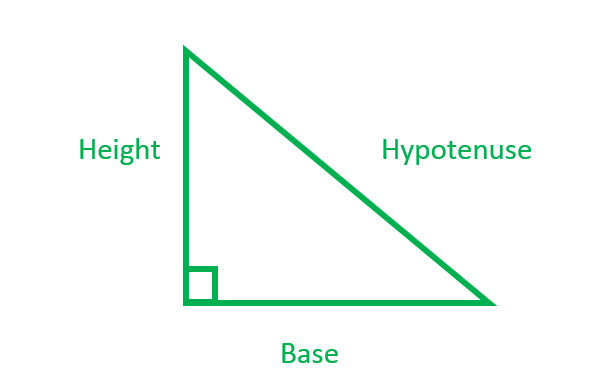
1. ∆ABC is Right-Angled
2. AD is Altitude
3. AE is Median i.e. E is the midpoint of BC

Proof:

(a+d)² = a² + (a-d)²

(a+d)² -(a-d)² = a²

a² + d² + 2ad – a² – d² + 2ad = a²

4ad = a²

a(a-4d) = 0

a – 4d = 0 (as a ≠ 0)

a = 4d (———-eqn. 1)

In ∆ABD

AB² = BD² + AD²

(a – d)² = BD² + AD²

(a – d)² = {(a + d)/2 – DE}² + AD² (———-eqn. 2)

In ∆ACD

AC² = DC² + AD²

a² = DC² + AD²

a² = {(a + d)/2 + DE}² + AD² (———-eqn. 3)

From eqn. 2 & 3, we get

(a – d)² – a² = {(a + d)/2 – DE}² + AD² – {(a + d)/2 + DE}² – AD²

(a – d +a )(a – d – a) = {(a+d)/2 – DE + (a+d)/2 + DE}{(a+d)/2 – DE – (a+d)/2 – DE}

(2a – d)(-d) = (a + d)(-2DE)

(2a – d)(d) = (a + d)(2DE)

So, 2DE = (2a – d)d/(a+d)

From eqn. 1, we get

2DE = (2*4d – d)d/(4d + d)

2DE = 7d²/5d

DE = 7d/10 = (4d + 3d)/10

But, AD = a –d = 4d – d = 3d & AC = a = 4d

Putting these values, we get

DE = (AC + AB)/10 (Hence Proved)